Using state machines and callbacks to model friction and limit stops
Modeling friction is always an annoying task, requiring extra characterization of your system and convincing modeling tools to operate through all the nonlinearities of the model.
Here we'll make a state machine to think about the different states of the model and then use the VectorContinuousCallback feature of the Julia DifferentialEquations.jl package.
Consider a sliding mass system in which an external force is applied to the mass and the mass is subject to static and kinetic friction, and bounded by limit stops which abruptly stop its motion.
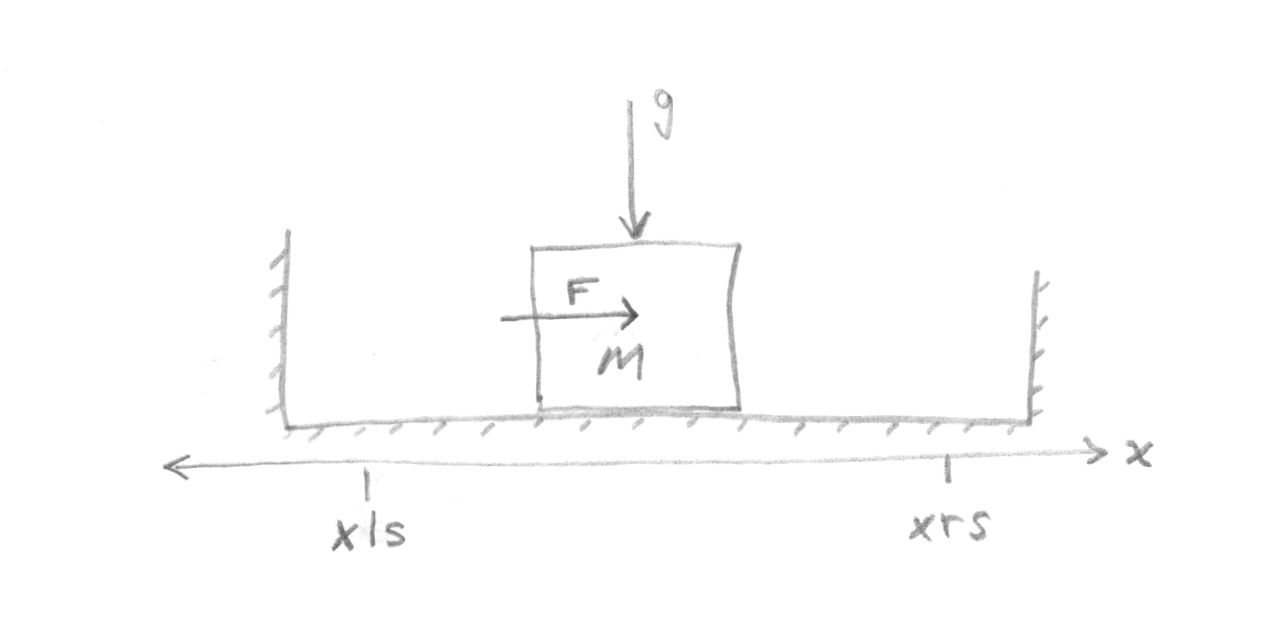
We can identify five different states for the system:
LEFT_STOP: mass against left stop, motion resisted by static friction and stopSLIDING_RIGHT: mass moving, being resisted by dynamic frictionSTOPPED: mass not against either stop, motion resisted by static frictionSLIDING_LEFT: likeSLIDING_RIGHTbut in the other directionRIGHT_STOP: likeLEFT_STOPbut at the other end.
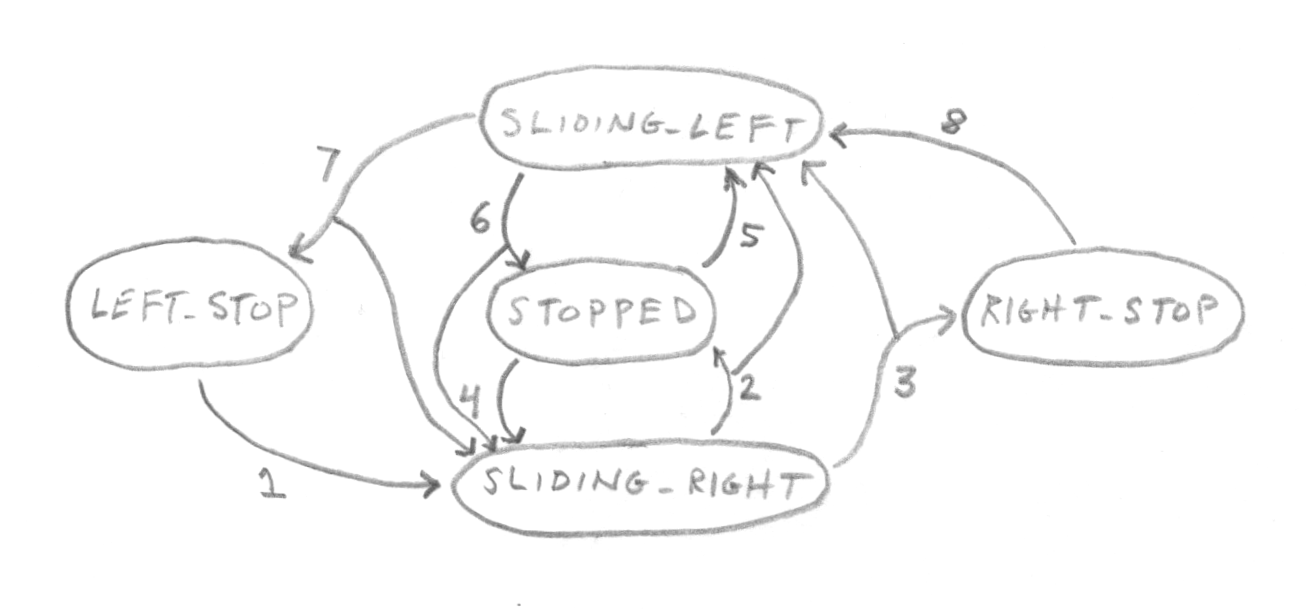
There are twelve transitions between states, organized in eight lines:
LEFT_STOPtoSLIDING_RIGHTif force (on the mass) is greater than static frictionSLIDING_RIGHTtoSTOPPEDorSLIDING_LEFT(depending on force) if speed drops to zeroSLIDING_RIGHTtoRIGHT_STOPorSLIDING_LEFT(depending on COR) if position reaches right stopSTOPPEDtoSLIDING_RIGHTif force is greater than static frictionSTOPPEDtoSLIDING_LEFTif force is greater than static friction (but in the other direction)SLIDING_LEFTtoSTOPPEDorSLIDING_RIGHT(depending on force) if speed drops to zeroSLIDING_LEFTtoLEFT_STOPorSLIDING_RIGHTif position reaches left stopRIGHT_STOPtoSLIDING_LEFTif force is greater than static friction (but to the left)
Let's enumerate our states and make a default parameter object using some tools from Parameters.jl.
xxxxxxxxxx State LEFT_STOP SLIDING_RIGHT STOPPED SLIDING_LEFT RIGHT_STOPParamsxxxxxxxxxx mutable struct Params M::Float64 = 1.0 # mass of sliding object in kg ga::Float64 = 9.81 # gravitational constant, m/s^2 μs::Float64 = 0.8 # coefficient of static friction μk::Float64 = 0.5 # coefficient of kinematic friction cor::Float64 = 0.3 # coefficient of restitution, 0=inelastic, 1=elastic xls::Float64 = -0.5 # location of left stop in m xrs::Float64 = 0.5 # location of right stop in m state::State = STOPPED # state of systemendLet's write a state-aware differential equation.
sbode (generic function with 1 method)xxxxxxxxxxfunction sbode(u,p,t) v,x = u # unpacking state variables p # unpack parameters by name into function scope #netforce = calcnetforce(p, force_ext, t) if state==LEFT_STOP dv = 0.0 # not moving dx = 0.0 # not moving elseif state==SLIDING_RIGHT dv = 1/M*(force_ext(t)-M*ga*μk) dx = v elseif state==STOPPED dv = 0.0 dx = 0.0 elseif state==SLIDING_LEFT dv = 1/M*(force_ext(t)+M*ga*μk) dx = v else # state==RIGHT_STOP dv = 0.0 dx = 0.0 end [dv, dx]end The tests we use to move from one state to the other are defined in FricSMCondx.
FricSMCondx (generic function with 1 method)xxxxxxxxxxfunction FricSMCondx(out, u, t, integ) integ.p v,x = u out[1] = (state==LEFT_STOP)*(force_ext(t)-M*ga*μs) out[2] = (state==SLIDING_RIGHT)*(-v) out[3] = (state==SLIDING_RIGHT)*(x-xrs) out[4] = (state==STOPPED)*(force_ext(t)-M*ga*μs) out[5] = (state==STOPPED)*(-force_ext(t)-M*ga*μs) out[6] = (state==SLIDING_LEFT)*v out[7] = (state==SLIDING_LEFT)*(-(x-xls)) out[8] = (state==RIGHT_STOP)*(-(force_ext(t)+M*ga*μs))endThe corresponding actions are defined in FricSMaffect!
FricSMaffect! (generic function with 1 method)x
function FricSMaffect!(integ, idx) integ.p v,x = integ.u t = integ.t if idx==1 integ.p.state = SLIDING_RIGHT elseif idx==2 if force_ext(t) < -M*ga*μk integ.p.state = SLIDING_LEFT else integ.p.state = STOPPED integ.u[1] = 0.0 end elseif idx==3 if cor==0.0 integ.p.state = RIGHT_STOP integ.u[1] = 0.0 else integ.p.state = SLIDING_LEFT integ.u[1] = -cor*integ.u[1] end elseif idx==4 integ.p.state = SLIDING_RIGHT elseif idx==5 integ.p.state = SLIDING_LEFT elseif idx==6 if force_ext(t) > M*ga*μk integ.p.state = SLIDING_RIGHT else integ.p.state = STOPPED integ.u[1] = 0.0 end elseif idx==7 if cor==0.0 integ.p.state = LEFT_STOP integ.u[1] = 0.0 else integ.p.state = SLIDING_RIGHT integ.u[1] = -cor*integ.u[1] end elseif idx==8 integ.p.state = SLIDING_LEFT endendxxxxxxxxxxcb = VectorContinuousCallback(FricSMCondx, FricSMaffect!, nothing, 8); Create a forcing function.
force_ext (generic function with 1 method)xxxxxxxxxxforce_ext(t) = t<25 ? t/2*sin(2π*t/2) : (25-t/2)*sin(2π*t/2)Set up a sim function which sets initial conditions, timespan, parameters, and simulation options. We set dtmax = 0.01 because without it the solver skips forward too quickly.
sim (generic function with 1 method)xxxxxxxxxxfunction sim() u0 = [0.0, 0.0] tspan = (0.0, 50.0) p = Params() prob = ODEProblem(sbode, u0, tspan, p) sol = solve(prob, callback = cb, dtmax=0.01)endxxxxxxxxxxsol = sim();Plot the results! Here we can see the system being pushed back and forth by an amplitude-modulated sinusoidal force.
xxxxxxxxxxlet p1 = plot(sol, vars=[1], ylabel = "velocity, m/s") p2 = plot(sol, vars=[2], ylabel = "position, m") p0 = plot(sol.t, force_ext, ylabel = "force, N") plot(p0,p1,p2,layout=(3,1), link=:x, leg = false)endxxxxxxxxxxbegin using DifferentialEquations using Plots using Parameters using StaticArrays using PlutoUIendConclusions
The callback feature of the DifferentialEquations.jl package allows one to implement a state machine to change the behavior of a system by letting the user
Define a set of states,
Define the behavior of each state in the ODE function,
Define the conditions on which states will change in a conditions function, and
Define what changes occur to the simulation on each change in the affect function.
The user can in this way define highly nonlinear actions and systems with discontinuous derivatives without causing solver issues because the solvers are aware of the callbacks and do not try to solve across the callback points.
This Julia language document was prepared using the Pluto reactive notebook system.
David Klaffenbach, 2021-01-01.
Revised 2021-01-05.